Archives pour la catégorie maths

Les maths en 6ème : nouveau programme 2016 chez Génération 5 dans la collection i-Parcours

Publié le par
Répondre

Nous avons reçu très récemment le nouveau manuel de Maths de la collection i-Parcours pour la classe de 6ème édité par Génération 5. Un manuel de cycle 3 avec son environnement numérique . Déjà on a travaillé sur des problèmes avec des nombres décimaux….. histoire de voir ce que cela donnait !

manuel_iparcours_maths6eme Manuel iParcours Cycle 3 – Maths (6ème)

Manuel Maths 6ème, cycle 3, collection i-Parcours, nouveau programme 2016

Tout d’abord, pour présenter cet ouvrage, j’ai commencé par la fin : le lexique (avec l’essentiel des notions) et le formulaire .

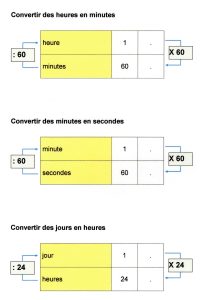
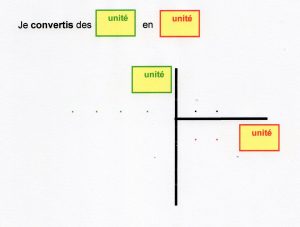
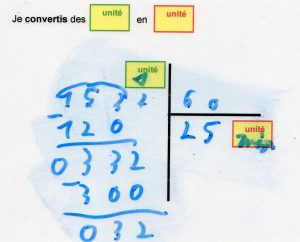
  1. Le lexique donne des définitions (exemple celle de l’hypoténuse dans un triangle rectangle) mais aussi des « explications » : comme faire une figure à « main levée », à « vraie grandeur » ou « intercaler » ou bien « convertir » …. Bref , ces mots sur lesquels on ne revient peut-être pas assez souvent, pensant qu’ils font partie du lexique « mathématique » de l’élève ……
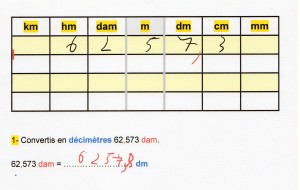
  2. Le formulaire , dernière page de l’ouvrage , comporte 5 parties : tableau de numération, préfixes, notations en géométrie, périmètres, aires, volumes et patrons : le minimum à avoir dans ses « outils mathématiques » sans doute

Le sommaire rappelle celui des cahiers d’exercices i-Parcours

On retrouve donc les 4 grandes parties : nombres et calcul, gestion de données, géométrie et grandeurs et mesures avec des chapitres identiques à ceux du cahier( présenté ici )

Les rubriques de chaque chapitre

Chaque chapitre est construit de la même façon , comme illustrée dans cette carte mentale avec de nombreux problèmes à résoudre , dans la continuité du CM2 , des exercices variés permettant à chacun d’avancer à son rythme :

manuel 6ème i-parcours MATHS rubriques de chaque chapitre

Un livre agréable, tout en couleur, clair, avec des personnages amusants qui présentent chaque chapitre (bravo aux illustrateurs !) et , si en plus, on peut éviter de le transporter à chaque cours grâce à la version numérique …..

Voici notre première utilisation la semaine dernière pour préparer une évaluation sur les opérations avec des nombres décimaux : la résolution de problèmes page 63 : un QCM (sauf que ….. Léo n’avait pas noté que les problèmes portaient sur …. les durées ….. d’où la cata à l’évaluation ….. ce n’est pas grave, ce n’est pas du temps perdu !! on reprendra les durées …. pendant les vacances ) .

Plusieurs possibilités :

  • un travail directement à partir du livre

qcm n°39

  • Mais pour limiter la quantité de données de la page, on a utilisé la version numérique : sur le manuel numérique en ligne , on a pris le même exercice et, avec l’outil « capture » nous l’avons mis sous OneNote : là, un seul exercice à l’écran, réponse avec le stylet ou au clavier directement ….. DONC plusieurs atouts : on peut sélectionner l’exercice voulu et en plus, on allège le poids du cartable …….
  • D’autres atouts de ce manuel numérique : des aides animées , des exercices interactifs (QCM pour se préparer au test et voir où on en est, activités sur tableur …) et le lexique et les formulaires toujours à disposition

Rappel : Nous avions déjà parlé des cahiers de Maths 6ème (CM1 et CM2 également)de cette collection i-Parcours ici et un nouveau cahier 2016 Maths 6ème sera disponible en septembre .Une collection très complète qui , pour le cycle 3 , tisse des liens entre les 3 niveaux concernés (CM1 , CM2 et 6ème)

 

 

 

la symétrie axiale sans quadrillage : une aide méthodologique

Publié le par
4

La symétrie axiale sans quadrillage est peut être plus « facile » à réaliser par Léo qu’avec des quadrillages. Tout simplement car :

  1. il n’y a pas cette surcharge visuelle des carreaux  
  2. le comptage des carreaux est toujours « coûteux » , lent : il en est toujours au même point et maintient qu’il y a par exemple une distance de 5 carreaux du point à l’axe quand il y en a 6 ou le contraire ….( la dyspraxie est bien tenace sur ce sujet chez lui) . De plus, au niveau « gestuel et spatial », Léo fait des « ponts » avec le doigt . Il a choisi de partir du point vers l’axe (et non le contraire) car ainsi il continue sur sa lancée (sur la même ligne …. ), système D sans doute …..
  3. tracer en gris (crayon à papier) sur le gris du quadrillage : il faudrait peut être aussi travailler en couleur …..

Nous avions donc une fiche méthode pour tracer le symétrique d’une figure dans un quadrillage (ici) et maintenant une nouvelle fiche pour faire ce tracer mais sans quadrillage .

J’ai repris le départ car Léo a toujours ce besoin (quadrillage ou pas) : avant de démarrer, comment je m’y prends ? et ,s’il saute cette étape, il peut oublier sa « méthode » :

  1. repasser les points (en couleur)
  2. choisir le point de départ pour construire le 1er symétrique

Nous utilisons la règle-équerre pour tracer la perpendiculaire à l’axe qui passe par le point puis le compas et enfin la règle pour tracer les traits. J’insiste auprès de Léo sur les outils nécessaires,l’ordre des actions car la semaine dernière en classe il a tenté une symétrie axiale sans quadrillage avec seulement l’aide du compas ( et ce n’était pas si mal finalement ….!!!! ).Voici donc la 2ème fiche méthode sur la symétrie axiale sans quadrillage :

sylvia480

Remarque : Il est vrai qu’il nous faut toujours « relancer » ces petits rappels lorsque l’activité n’a pas été reconduite depuis longtemps (comme ici depuis l’an dernier). Je vais essayer de réfléchir sur le « comment retrouver seul une procédure » sur des choses simples d’abord puis plus compliquées [peut-être est-ce « utopique » tant que la procédure n’est pas automatisée complètement ? Une procédure qui « paraît » automatisée à un moment T , résistera-t-elle au temps qui passe aussi ????? Un seul mot : faisons-leur confiance …..]

 

Convertir des durées : une fiche méthode pour organiser ses calculs

Publié le par
8

En CM1, nous avions déjà mis en place quelques outils sur la conversion de durée.

Cette année, lorsque Léo a redémarré cette activité, les difficultés ont réapparu et je l’ai senti « perdu » .En réfléchissant et avec l’aide de son orthophoniste, on a mis au point une « procédure ».

1er point : je cherche le nombre d’unités de temps (dans le nombre à convertir) et je les coche, cela me donne le nombre d’étapes

Les étapes sont indiquées et Léo doit compléter :1- je convertis ……. en …… , puis écrit son opération (il peut alors se servir de l’outil présenté en n°1 ci-dessus), 2- et ainsi de suite ….

Puis l’outil présenté ci-dessus pour la conversion de durées a été simplifié [une seule fiche déjà proposée ici MAIS nous n’avons plus utilisé la soustraction ni la calculatrice et opté pour la division qui est maintenant bien dominée] et un gabarit pour la division :

outil simplifié pour la conversion (à avoir sous les yeux) et gabarit division pour les heures:

img440 sylvia463

En images : exercice avec les étapes à compléter :

sylvia471

Remarque : pour la division, un petit gabarit permettant de mieux voir les unités m’a semblé utile : ainsi côté dividende ce sont des secondes donc le reste sera des secondes , côté quotient ce sont des minutes

sylvia472

Un exemple à 2 étapes :

sylvia473

Il me semble que Léo a encore besoin de s’entraîner avec cette nouvelle procédure mais nous manquons un peu de temps ….

la division décimale : un (ou 2)nouveau(x) gabarit(s) à essayer

Publié le par
2

Nous sommes en plein dans la division décimale : cette division , qui a un reste , nous amène à « ajouter des zéros » au dividende (chiffre des dixièmes, centièmes , millièmes quand c’est nécessaire) . Après la leçon faite en classe, j’ai préparé un gabarit de division décimale mais Léo se repère déjà bien dans la pose de cette opération . Il va falloir « automatiser » les 2 opérations simultanées : j’abaisse le 0 des dixièmes et je mets une virgule au quotient (la 1ère fois Léo voulait ajouter une 2ème virgule quand il a abaissé le 0 des centièmes ….) .

Quelques explications à donner, et sans doute à répéter …. :

  1. Lorsqu’il y a un reste à la division et que l’on veut partager ce reste alors on va faire une division décimale
  2. Dès que je commence à partager le reste : je « descends » le 0 des dixièmes et j’écris une virgule au quotient (Remarque : on utilisera cette même procédure lorsque le dividende sera un nombre décimal , on « descendra » le chiffre des dixièmes et on écrira une virgule au quotient)
  3. Se demander si c’est nécessaire, utile, possible …. de toujours continuer la division (mettre une virgule et des dixièmes, centièmes …..). Ainsi, si on partage des € , on peut aller aux centièmes [ce sont les centimes d’€ , donc 2 chiffres après la virgule suffisent : 13 € : 4 = 3,25 €) . Mais peut – on parler de 3,25 boîtes de crayons ? J’ai 13 crayons à ranger dans des boîtes de 4 crayons donc 13 crayons : 4 = 3 boîtes et il reste 1 crayon là on s’arrêtera à une division à quotient entier et on indiquera le reste .

2 gabarits ( 2 chiffres au dividende ou 3 chiffres)

sylvia458 sylvia459

ou à télécharger sous Word gabarit division décimale 3 gabarit division décimale 4

P1080481

Mais aussi , un gabarit à tester chez « Le petit roi » en suivant ce lien . Je l’ai utilisé en « coloriant) la partie décimale du dividende et les colonnes correspondantes : Léo se répérant assez facilement dans cette opération, nous l’essaierons aussi sous la forme suivante :

sylvia467

à télécharger sous Word autre gabarit d’après petit roi

C’est lui qui fera son choix …… on doit s’entraîner en fin de journée ( peut-être !)

 

Les cahiers de Maths i-parcours chez Génération 5

Publié le par
7

Nous avons reçu 3 cahiers de Maths collection i-parcours de chez Génération 5 niveau CM1, CM2 et 6ème et bien sûr, aussitôt arrivés, nous les avons utilisés directement pour faire quelques entraînements en lien avec ce qui était fait en classe .

Au premier abord, des cahiers très agréables « à l’œil »:

  • colorés, clairs, qui nous rappellent les cahiers « Sesamath » que l’on connaît un peu déjà.
  • Une famille Renard que l’on retrouve en tête de chapitre et au cours de certains exercices
  • des exercices très variés pour aborder la notion sous différents angles
  • une « continuité » dans la présentation que l’on retrouve par exemple du cahier CM1 au cahier 6ème , donc des repères vite pris et retrouvés facilement
  • des problèmes dans chaque chapitre et un chapitre particulier réservé à la résolution de problèmes

Ce qui est aussi très intéressant , c’est qu’on peut utiliser ces cahiers quels que soient le manuel ou la leçon présentée en classe . Soutien, entraînement , révisions …. tout est possible .

Par exemple, des exercices sur les opérations de nombres décimaux ( tout au début de la notion) pris dans le cahier 6ème (il fallait bien commencer par celui-ci même quand on est encore en CM2 !) et réalisés directement sur le cahier :

sylvia420 sylvia421

Pour d’autres exercices, nous avons choisi la version « cahier numérique » qui nous permet :

  • de sélectionner 1 exercice :  choisir « complément d’exercice : affichage de l’énoncé de l’exercice » .Puis, à l’aide de l’outil « capture » (merci à Dominique de Génération 5 qui nous a donné la marche à suivre !) , coller sous OneNote et  réaliser le travail directement (au stylet et/ou au clavier) après l’avoir agrandi (grâce à l’écran tactile), surligné les données importantes, fait un schéma …. Ce qu’il n’est pas possible de faire sur le cahier (par manque de place, police plus petite, exercices plus serrés … comme dans les manuels d’ailleurs ; là on peut donc isoler l’exercice et le réaliser sans avoir d’autres informations en même temps sous les yeux).

Quelques exemples issus du cahier CM2 (toujours sur les décimaux) :

sylvia422

fait sous OneNote avec une ligne graduée « simplifiée :sylvia425

ou un coloriage fait avec le stylet ( attention Léo a pris du bleu à la place du orange et , pour gagner du temps et « s’économiser » ,une marque de couleur remplace le « coloriage de la case » ….ce n’est pas une mauvaise lecture de consigne) , Léo ayant pu agrandir le dessin à l’écran (ensuite bien sûr, le travail peut être rendu à l’enseignant sous la forme A4 , soit sur une clé, soit imprimé en classe si imprimante à disposition ….) : [Remarque : une seule partie de l’exercice a été faite car Léo barre au fur et à mesure les nombres qui ne répondent pas à la première consigne , l’ensemble deviendrait alors « trop chargé » et source d’erreur pour faire la 2ème consigne. Si on veut la faire, je reproposerai le coloriage du départ avec seulement la 2ème consigne .]

sylvia423 sylvia426

Ou un problème toujours dans le même chapitre sur les opérations de décimaux .Le problème a été « adapté » : c’est-à-dire ici, j’ai préparé les débuts de phrase qui guident sa démarche de résolution de problème . [Actuellement Léo SAIT et PEUT écrire tout cela seul (et à la main car c’est son souhait) MAIS afin de bien installer ce type de résolution de problèmes comprenant des étapes (et questions intermédiaires implicites), on « supprime » un coût (attentionnel …) et on lui laisse toutes ses facultés de résolution en indiquant finalement peu de choses … ]

sylvia424 sylvia427

  • MAIS AUSSI de faire des choses beaucoup plus importantes :
  • consulter des aides animées (exemple ici : addition et soustraction de décimaux) : on écoute et en même temps on voit comment faire ou comment ça marche ….. On en trouve dans tous les chapitres.
  • répondre à des QCM lorsqu’on prépare une évaluation par exemple : là c’est un QCM de chapitre ou QCM d’évaluation  ou bien un QCM lié à une page d’exercices et là ce sera un QCM d’entraînement : on peut donc toujours « vérifier » ou l’on en est , rapidement
  • Dans le chapitre « Résolution de problèmes », l’énoncé est souvent lu (pour éviter les difficultés liées à la lecture) mais d’autres aides originales sont souvent proposées : un QCM préparatoire à l’exercice et une aide animée qui permet de mettre des « images » sur la situation présentée.
  • Pour les enseignants, accès aux corrections de tous les exercices avec parfois des corrections animées (notamment en géométrie par exemple dans le chapitre des angles où tous les exercices sont corrigés avec des animations) très « parlantes » .

Finalement des cahiers très « riches », faciles à utiliser, facilement « adaptables » aussi, qui permettent de travailler les différentes notions vues en classe. L’idéal : avoir le cahier en classe ainsi que la « permission » de naviguer du support papier au support numérique comme nous pouvons le faire à la maison , ce serait le TOP ! car on est au cœur de la complémentarité papier / numérique à laquelle nous tenons particulièrement .

Une vue d’ensemble du fonctionnement des 3 cahiers de la collection i-parcours Maths CM1, CM2, 6ème en carte :

Cahier d'exercices i-parcours MATHS CM1 CM2 6ème

Tous ces cahiers sont à découvrir chez Génération 5 , des vidéos très claires sur la version élève ou la version professeur sont disponibles aussi sur le site de « i-parcours » . Et bien sûr , les cahiers et manuels collège sont prévus pour juin et septembre 2016 . On peut déjà consulter quelques pages en ligne.

cahierdemaths6ème Cahier d’exercices MATHS 6e (collection iParcours)

cahierexerciesmathscm1 Cahier d’exercices MATHS CM1 (collection iParcours)

cahierexercicesmathscm2 Cahier d’exercices MATHS CM2 (collection iParcours)

Les manuels de Maths de la 6ème (nouveaux programmes 2016)  à la 3ème seront bientôt disponibles (visibles en juin) et nous aurons la chance de recevoir un manuel 6ème que nous aurons le plaisir de présenter .

Dans un prochain article, nous parlerons aussi des cahiers i-parcours en Français, niveau 6ème actuellement disponible ….

Une collection à suivre donc …..

Ajout du 27/05 : Une petite précision concernant l’accès aux corrigés pour les parents qui nous l’ont demandé (notamment ceux qui font de l’IEF) : il vous faut contacter Génération 5 à l’adresse suivante : enseignement@generation5.fr

 

 

Maths : un petit tour du côté de Singapour …..

Publié le par
4

Nous publions aujourd’hui le travail d’un collègue belge, Marc (prof de math) qui est en charge d’élèves de 15 à 18 ans, avec handicap « dys » et autres. Il utilise en Maths la méthode de Singapour ( livres que l’on peut se procurer à la Librairie des Ecoles ou sur Amazon par exemple) et l’ a présentée à ses collègues . Il nous fait profiter dans un premier temps du concept de tout et partie à l’aide de 2 cartes mentales qu’il a créées en reprenant le déroulé d’une séance décrite dans le guide pédagogique de l’éditeur.

SING 1

SING 2

cartes en pdf séance 2-1a CE 2ème partie séance 2-1a CE2 1ère partie

Marc nous a précisé que « le guide est un outil fort utile pour mener à bien la démarche de raisonnement. Une bonne verbalisation de la pensée qui consiste à décrire, expliquer les étapes qui permettent de résoudre des problèmes. La verbalisation justifie un raisonnement afin de pallier à une approche souvent « directe, impulsive » de l’élève, ce dernier ne faisant pas attention aux données mathématiques en jeu dans le problème. »

Merci Marc pour ton partage …. D’autres cartes à venir …..

En image quelques livres de la « Collection » qui s’étend du CP au CM2 , livres ou cahiers de l’élève, guide pédagogique par niveau ou plus généralement sur la méthode et même un fichier pour la GS de maternelle …..
 Manuel de mathématiques CM2 : Méthode de Singapour
Mathématiques CP-Méthode de Singapour-Fichier de l’’élève A

un exemple pour le CE2 : un manuel, 2 cahiers d’exercices et un guide pédagogique
 Manuel de mathématiques CE2 : Cahier d’exercices B
 Manuel de mathématiques CE2

 Guide pédagogique CE2

Un retour sur les problèmes de partage et groupements

Publié le par
2

Nous avons déjà pas mal abordé ce sujet des partages ici et là … ET POURTANT il y a bien encore des « zones floues » me semble-t-il ….. J’ai donc essayé de reprendre le sujet avec quelques modifications pour voir si le chemin serait plus aisé , plus efficace aussi .

S’interroger sur le type de partage : que recherche-t-on exactement ?

2 possibilités ( on pourra revoir la carte mentale qui « résume » ces situations de partage ici ) : on cherche :

  1. la valeur d’une part ?
  2. OU le nombre de parts ?

Encore faut-il avoir analysé l’énoncé , ce qui n’est pas si simple ……

Voici la procédure que j’avais essayé de mettre en place l’an dernier mais par manque de temps d’une part, et comme ce n’était pas la procédure employée en classe d’autre part, je n’avais pas insisté .On peut la retrouver dans l’article : un problème résolu « trouver la valeur d’une part » .

Cette année, il y a une démarche « écrite » pour annoncer ce que l’on cherche et ce que l’on va calculer pour y arriver AVANT d’attaquer ses calculs . Ceci est très intéressant car :

  • on freine  l’impulsivité
  • on permet de « poser » par écrit AVANT de démarrer donc cela permet de se rassurer et de décharger le « niveau attentionnel » : tout est là , écrit et ne disparaîtra pas
  • on est alors en mesure de faire ses calculs et de revenir sur ce qu’on a écrit si on « se perd »
  • et finalement le travail par écrit en Maths (accompagné de la verbalisation de ce qu’il fait) aide Léo : il demande déjà pour la 6ème de « faire les maths à la main » ….( cela a d’ailleurs été sa volonté depuis le CE1)

Il me semble nécessaire de travailler « quotidiennement » cette démarche écrite de résolution de problèmes qui finalement lui permettra d’écrire sa propre « procédure » et de s’y tenir lors de la résolution de problème. [Une idée à ajouter dans notre programme d’expressions  jusqu’à la fin de l’année : 1 problème à résoudre par jour ]

Voici la fiche avec laquelle nous allons essayer de travailler pour analyser la situation de partage en associant les gestes (empruntés au livre de B.Gueritte L’enfant et le temps): le zoom avec les œillères pour aller chercher le 1 (reprise légèrement modifiée « trouver la valeur d’une part ») ici, on a tout sous les yeux , et on va mettre l’image suivante :sylvia300

ou la main qui prend les objets pour faire des tas,  des parts identiques , des sacs …. pour « trouver le nombre de parts » , un problème de « groupement » avec l’image suivante :sylvia298

Mais avant tout ,nous sommes repassés par  le « je connais le tout » symbolisé par une sorte de cercle où les mains sont attachées (geste) : c’est sur ce tout que l’on va travailler ( c’est ce tout que l’on va partager…..)

sylvia281

fiche à télécharger sous Word Dans les problèmes de partage fiche méthode

Des exemples sur des problèmes – types qui pourront servir de « modèle dans notre classeur de problèmes résolus »:

sylvia283sylvia282

et un peu plus compliqué puisqu’il faut d’abord trouver ce « fameux tout » avant de partager (problème à 2 étapes ) :

sylvia284

Après un premier essai avec Léo, voilà les problèmes résolus que nous conserverons dans notre classeur (à la place de ceux de l’an dernier) : ici quelques-uns en images (tous sont à télécharger sous Word ci-dessous : rappel : je me suis servie depuis l’an dernier pour le classeur de problèmes résolus du travail de Mallory et de sa présentation ici)

problèmes de nombre d’objets / partage : recherche de la valeur d’une part

sylvia291sylvia292

problèmes de prix / partage : recherche de la valeur d’une part

sylvia293sylvia294

problèmes de nombre d’objets / groupement : recherche du nombre de parts 

sylvia295sylvia296

problèmes de prix / groupement : recherche du nombre de parts 

sylvia297sylvia301

à télécharger sous Word P1 groupement, objets p1-partage-valeur-dune-part-objets1 P2 groupement, prix p2-partage-valeur-dune-part-prix1

 

 

 

Les fractions (4 et fin ?) : somme d’un nombre entier et d’une fraction <1

Publié le par
8

FRACTIONS toujours , peut-être le dernier article sur ce sujet cette année …… Une autre compétence à acquérir avec les fractions :

écrire une fraction sous la forme d’une  somme d’un entier et d’une fraction inférieure à 1 :

nous sommes passés par la manipulation à mon avis « indispensable » pour voir et comprendre comment cela fonctionne (j’avais fabriqué « les familles de demis, de tiers, de quarts et de cinquièmes » en téléchargeant directement les documents chez le petit roi ici, et nous avons transformé des fractions en nombres entiers ou en somme d’un nombre entier et d’une fraction inférieure à 1 – sans oublier de passer par l’opération contraire ! – ). Des fiches sont toutes prêtes pour s’entraîner (Merci encore à la maman du petit roi pour tous ces partages) .

Pour la manipulation, on peut aussi s’inspirer des fractions en pâte Fimo (voir sur la page Facebook du blog , avec une photo à l’appui de Delphine : une idée géniale !)

Nous avons revu à nouveau nos « pizzas » ( par exemple : 5/4 de pizza c’est une pizza entière et un quart ). On est passé de ce que l’on a manipulé, vu (ou dit) à une écriture mathématique finale de type (pour l’exemple ci-dessus) : 5/4 = 4/4 + 1/4 = 1 + 1/4.

Une fiche méthode pour aider à automatiser la démarche : ( à revoir éventuellement selon l’usage qu’en fera Léo et la nécessité ou non ….)

sylvia166

J’ai conservé pour l’adaptation des exercices la dernière ligne de la fiche méthode qui fait apparaître la décomposition . Un exemple sur un des premiers exercices fait en classe :

sylvia165

Remarque : ce type d’exercice ne semble pas être « coûteux » pour Léo en raison (à mon avis) de sa très bonne connaissance des tables et surtout à la « manière » dont elles ont été mémorisées dès le départ (avec une installation « spatiale » et une « dynamique » avec l’opération inverse entre autre …) – Merci encore à l’orthophoniste de Léo –

Rappel pour s’entraîner en ligne sur ce sujet : toujours sur Sesamaths CM2 (page 20 avec le n° 1 en correction animée ) . Pour revoir les fractions, un logiciel sur le site de logicielspedagogiques à télécharger ici : « Ce petit outil permet de découvrir les fractions ainsi que de travailler sur les fractions équivalentes ». Nous allons essayer de le regarder dans la semaine …..

Et pour finir , une sorte d’outil de référence sur les droites graduées qu’il me semble bon d’avoir « sous la main » , donc dans la pochette en classe et dans l’ordinateur (on devrait pouvoir l’utiliser sous OneNote avec le stylet . Je l’ai fait en 2 versions : l’une à conserver, l’autre pour s’entraîner. Je suis volontairement partie sur des mêmes bases concernant :

  • l’ unité ( la même au niveau de la « longueur » ) qui va être ensuite partagée
  • la droite avec un départ 0 visible (on n’est pas dans un « ajout » de difficulté puisqu’il s’agit d’une base)
  • le 0 et le 1 sont toujours indiqués en rouge et en gras (les entiers étant écrits en dessous de la droite graduée)
  • une place « prête » (rectangle rouge) pour indiquer la valeur du 1 dans chaque droite, en fraction
  • un point bleu bien visible qui situe la valeur d’une part avec une case bleue au-dessus pour écrire la fraction
  • le petit pont qui visualise aussi une part
  • sans oublier la phrase écrite au-dessus de chaque droite graduée :  « L’unité est partagée en … parts égales, en ….. « 
  • Remarque : j’ai « amorcé » les décimaux avec une droite pour noter les décimaux (allant au chiffre des dixièmes) …..

en images : la version outil de référence à conserver

sylvia170 sylvia169

la version pour s’entraîner

sylvia168sylvia167

à télécharger sous Word (tout ce qui est surligné, les ponts … sont ajoutés à la main !)droites graduées référentiel

En espérant avoir fait le tour ( ou une fraction du tour) des fractions ……

Les Fractions (3) : fraction et nombre entier

Publié le par
3

Après quelques réflexions sur le retour des fractions (Fractions 1 ici et fractions 2 là) , nous avons continué nos manipulations avec les fractions ( la fraction du jour est plutôt devenue la fraction de la semaine car il n’y a pas que des fractions au programme ….. et il n’est pas toujours possible de trouver du temps ….)

Encore des astuces et/ou fiches méthodes :

Fraction égale à un nombre entier

Tout d’abord , dans quel cas une fraction est-elle égale à un entier ? Retour sur nos pizzas et les remarques qui en ont découlé  : pour cela, nous avons regardé à nouveau le travail effectué sur la fraction 1/4 (ici) . Mais là aussi, grâce à la connaissance des tables , la partie calcul va très vite ….Donc il n’a pas été utile de passer du temps sur cette notion. Nous reviendrons quand même de temps en temps à la manipulation et reverrons également cela dans la droite graduée …..

exemple en image, en classe :

sylvia163

encadrer une fraction par 2 entiers consécutifs 

Après plusieurs essais , voici la fiche méthode qui semble convenir à Léo :

sylvia135

On pourra l’alléger ou bien s’en servir sans tout remplir au cours de l’exercice donné. Finalement, elle nous aura été utile au début pour décomposer la tâche (comment je vais m’y prendre?), mais comme les tables sont très bien sues , Léo s’en est vite passé. Il commence par écrire l’encadrement en fraction (ici en 3ème étape) puis écrit de chaque côté le nombre entier correspondant en me disant (fièrement … ) »Je n’ai pas besoin de la fiche méthode » . Mais, nous y reviendrons sans doute dans quelque temps , pour vérifier, en cas de stress, de fatigue et aussi pour limiter  son impulsivité ……

exercice fait en classe , sans la fiche méthode :

sylvia164

Remarque : On a pris aussi le temps (et on va le refaire d’ailleurs) de remettre une droite graduée sous les yeux quand le travail est fini afin de faire des liens entre ces différentes écritures et/ou représentations .

Un exemple en image avec l’encadrement de la fraction 49/5 :

sylvia137 sylvia162

On peut y ajouter une nouvelle fiche méthode d’aide au placement d’une fraction sur une droite graduée, sans l’origine 0 visible, quand on connaît son encadrement , toujours  afin de faire des liens entre toutes ces représentations.

Remarque sur cette fiche : La droite graduée est prête MAIS il faudra que l’enfant place une unité ( seuls un trait et une graduation apparaissent) afin de bien passer par la démarche « cette unité est partagée en …. ». On peut aller jusqu’au dixième, ce qui pourra être utile pour placer des nombres décimaux plus tard ( avec un seul chiffre après la virgule) sur une ligne « aérée » sur la forme ….

à essayer ….. et certainement à reprendre ….. en prenant le temps de faire toutes les étapes …. (à mon avis )

sylvia161

 

 

 

 

Mesures, conversions, virgule et tableau : comment s’entendre ?

Publié le par
6

En ce moment Léo travaille sur les mesures donc sur les conversions .

Avant d’aborder les conversions dans les problèmes, il s’agit de bien reprendre les conversions dans le tableau de numération. Actuellement, la méthode utilisée dans le manuel de la classe est la suivante :

sylvia129

Or Léo n’a jamais fonctionné ainsi. Voici comment il procède sur ce même exemple :

  1. 62,573 dam  : on repère l’unité de mesure le dam et on place la virgule dans la colonne des dam
  2. on écrit alors le nombre tel qu’on le voit
  3. pour le convertir en dm, on efface la virgule de départ et on l’écrit à sa (nouvelle) place (dans la colonne des dm)

Remarques : Le fait d’essayer de « modifier » sa démarche l’a, me semble-t-il, un peu « embrouillé », du moins « déstabilisé » . Nous allons reprendre ce week-end et faire à nouveau verbaliser sa technique mise au point en CM1. Bien sûr, chaque enfant trouvera « sa » technique surtout que celle-ci est valable dans toutes les conversions …..

Quant au tableau de conversion, il me semble aussi préférable de le conserver , cela permettant aussi de « tempérer » l’impulsivité puisqu’il faut faire son travail dans le tableau puis le recopier sur sa fiche, Léo étant très rapide sur ce genre de manipulation( passage de la fiche plastifiée à la réponse sur le cahier ou la fiche)

On a essayé aussi  sur l’ordinateur avec le stylet sous Word et le tableau de conversion du ruban du cartable fantastique  :

  1. Insérer le tableau SOUS l’exercice [comme on le ferait pour une feuille de conjugaison] ( à voir pour éviter le balayage ce qui convient : juste sous le 1er exercice demandé ou pour chaque exercice  …..)
  2. Avec une 1ère couleur : placer la virgule (colonne de l’unité de mesure), et écrire le nombre
  3. Avec une autre couleur, effectuer la conversion ( nouvelle virgule , des 0 supplémentaires, rien juste à prendre le nombre en entier …. )
  4. Effacer la virgule (au doigt ou au stylet)
  5. Recopier son résultat (avec le stylet)

En image:

sylvia132

Les avantages :

  1. Le tableau reste et l’enseignant le voit (au lieu d’effacer sur la fiche plastifiée) / retour et correction / explication possibles OU suppression du tableau après utilisation possible ( pour éviter de nombreuses feuilles à imprimer SAUF si l’enseignant effectue la correction sur l’ordinateur (ou sur la clé USB qui enregistre le « cahier de maths virtuel »)
  2. Pour le collège OU un exercice sur les mesures non adapté [OU si l’enfant n’a qu’ 1 seul bureau en classe : difficile d’utiliser à la fois le cahier et l’ordi sur la même table, chute de matériel «assurée» ! Réfléchir dès maintenant à ce problème : passage progressif à « tout ORDI ? »] : Léo saura ainsi avec son ordinateur trouver l’outil dont il a besoin (tous les tableaux de conversion sont présents)

Remarque : la maîtrise du stylet est en cours et Léo aime cet outil (couleurs, choix …. , rapprochement du stylo et donc du travail à la main ….) De temps en temps , l’outil nous joue des tours MAIS il est relativement performant quand même et le doigt a aussi un rôle à jouer ! Et finalement le « technicien en herbe » se débrouille ….. On essaie tout de même de faire chaque soir un court exercice demandant l’utilisation du stylet (corriger , …),d’utiliser le passage en mode tablette ou en PC « incliné » …. On recherche les meilleures positions pour lire et écrire de la manière la plus efficace possible afin d’utiliser au mieux les performances de son nouvel ordinateur !

D’autres remarques possibles au niveau des adaptations :

  • mettre en rouge (et/ou en gras) l’unité de mesure donnée et celle dans laquelle on souhaite la conversion
  • réécrire à chaque ligne les unités de mesure (car cela permet d’avoir tout le temps les unités de mesure données ou demandées sous les yeux) au lieu de l’écrire seulement une seule fois dans la consigne (c’est d’ailleurs plus exact en écriture mathématiques)