C’est encore un problème « d’actualité » pour Léo. Il est assez « simple » d’analyser les difficultés ou plutôt les obstacles à la réalisation de ces différents travaux et donc mon objectif est d’essayer de trouver des astuces, des aides, des adaptations, des contournements, des compensations ( en allant crescendo !) pour un enfant qui aime la géométrie, qui sait (maintenant) bien utiliser les outils (règle, règle-équerre, compas) MAIS qui :
- peut facilement être perturbé par un support trop chargé (exemple : trop de droites parallèles , sécantes …. dans une même figure)
- a du mal avec les angles présentés « attachés par un même sommet »
- est gêné pour démarrer un exercice qui comprend beaucoup de lignes « obliques » .
- …….
Il faut de plus « accepter » :
- que la précision n’est pas toujours au rendez-vous malgré une très grande application (gourmande en réserve attentionnelle d’où une difficulté supplémentaire en évaluation où l’on demande plusieurs exercices , à la suite, qui font appel à des « stratégies » différentes ….)
- qu’il y a en géométrie des tas de « petites choses » à ne pas oublier et pas toujours automatisées: codage de la figure, nommer les figures et ou les droites (utilisation des signes, des lettres en capitales ou non ….)
- ….
- que si on met en place une « procédure » , il faut qu’elle soit utilisée bien en amont pour être efficace au moment de l’évaluation , qu’elle ait été « automatisée » par l’enfant ou qu’il puisse encore utiliser un outil d’aide (à la planification, au codage …..) tant qu’il en a besoin .
Même si mon « analyse » est loin d’être complète et que l’on découvre souvent les difficultés « après l’exercice ou après l’évaluation » , que proposer ? Que peut-on demander en classe ?
Quelques « astuces » dans 3 types de situations rencontrées :
- réaliser une figure en suivant un programme de construction ,
- trouver la figure correspondant à un programme,
- reproduire une figure (et c’est sans doute le plus difficile pour Léo …) .
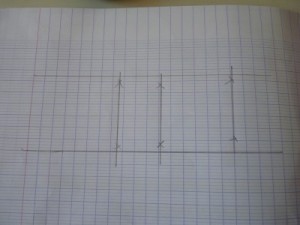
1- Suivre un programme
- Plus le programme est long, plus c’est compliqué surtout si les différents tracés se coupent , si un manque de précision ne permet pas la réussite de l’étape suivante ….
Une aide possible :
- scinder le programme en 2 sous-programmes
- les étapes doivent être clairement indiquées (aller à la ligne à chaque étape ou sous-étape)
- préparer une case à cocher à chaque étape , parfois nécessité aussi de faire plus d’étapes (une consigne par étape, très claire )
- écrire en entier : la droite (AB) , le segment [AB] car le codage seul peut être source d’erreur
- laisser à portée de mains les « fiches méthodes » de rappel de construction (si nécessaire) ou faire verbaliser la démarche si l’enfant « bloque »
- préciser le matériel à utiliser (surtout si l’enfant utilise des outils différents – exemple la règle-équerre – ceci pouvant être noté en haut de la fiche)
- un exercice par page
- on peut préciser si des points déjà utilisés doivent être à nouveau utilisés dans une autre étape
- un exemple (« adapté » à partir d’un exercice trouvé sur internet chez ???)

2- Trouver la figure correspondant à un programme
Un exemple de travail (trouvé aussi sur internet) en image ( avec une première adaptation sur la forme – police, couleurs, un exercice par page):

Une question se pose : comment vais-je m’y prendre ?
Une aide possible : (planifier la tâche donc une adaptation sur le fond cette fois)
- Je lis le programme en entier
- puis par étape : pour chaque étape, je vérifie chaque figure ( étape 1 : il y a bien un carré tracé dans les 3 premières figures MAIS pas dans la dernière)
- et je barre la (ou les figures) qui ne respecte(nt) pas le programme
- je passe ensuite à l’étape suivante …..
Une fiche procédure à essayer : Quelle figure correspond au programme ? fiche méthode avec un exemple au verso


Nous avons testé ce matin et simplement en suivant la fiche méthode , en s’arrêtant à chaque étape (et même au début, en cachant les étapes suivantes pour ne laisser apparaître que l’étape étudiée), le résultat a été parfait , la preuve en images :

3- Reproduire une figure
Là aussi, la difficulté sera souvent liée au « Comment je vais m’y prendre? » , « dans quel ordre ? » …. et surtout comment éviter de partir de manière impulsive ,sans savoir où l’on va ….
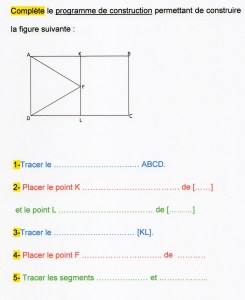
Il semblerait intéressant, avant d’apprendre à reproduire une figure , de passer par un programme de construction à compléter comme dans l’exemple ci-dessus (trouvé aussi sur internet chez ??? et adapté sur la forme)
 et là , encore une surprise :
et là , encore une surprise :
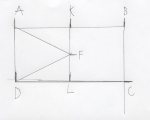
J’ai demandé à Léo , sans lire la fiche, de regarder , observer cette figure et de me la décrire . Ce qu’il voit en premier ( ce qu’il a repéré au premier coup d’oeil, donc ce par quoi il commencerait sa reproduction) n’est pas le grand rectangle ABCD (vu par « la mathématicienne » que je suis ou sans doute comme une grande majorité d’enfants) MAIS le triangle AFD …… Voilà donc comment, tout simplement, il peut partir dans une reproduction de figure pratiquement impossible à son niveau . (Cela m’a rappelé la figure de Rey à reproduire chez le neuropsy il y a 3 ans , qui avait été catastrophique avec le modèle et meilleure sans modèle, en restitution de mémoire visuelle!)
Il a poursuivi par les rectangles AKLD et KBCL et j’ai dû lui poser la question : « et la figure ABCD c’est quoi ? » un rectangle ajoute-t-il immédiatement …. Mais celui-ci est donc nommé en dernier ….et après ma question ….
Il a rempli ensuite correctement le programme ….

Et, figure cachée, deux jours plus tard, je lui ai demandé de tracer la figure en suivant le programme et en cochant les étapes de construction au fur et à mesure . Puis, nous avons vérifié avec le modèle de départ. Résultat en images : parfait ! cochage des cases à chaque étape donc un avancement du travail sans aucune impulsivité , tout était bien contrôlé (revoir le point n° 1 : suivre un programme ….. ça marche !)




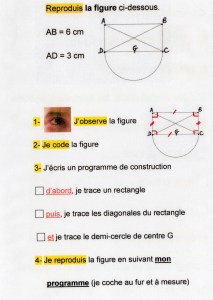
Une aide possible en guidant l’observation et en faisant écrire le programme
- J’observe la figure
- Je code la figure (angles droits, longueurs, égalités ….)
- J’écris mon programme ( on peut aider au début par une trame …. ou vérifier l’écriture de ce programme , voir s’il ne manque rien …., si le choix de l’étape 1 est réalisable …)
- Je reproduis la figure en suivant mon programme
Une fiche procédure à essayer : Comment reproduire une figure ? fiche méthode avec un exemple au verso

Remarque : Il faudra peut-être aussi donner l’étape 1 pour que Léo démarre correctement : par exemple ici je trace un rectangle ABCD ( ou plutôt lui faire verbaliser le début de son programme pour s’assurer qu’il ne démarre pas d’un endroit impossible à construire (actuellement du moins) …)
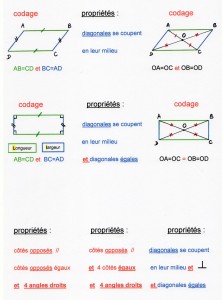
Rappel : des aides en géométrie sur le vocabulaire et le codage ici et là













































![IMG_5966[1]](https://fantadys.com/wp-content/uploads/2014/10/img_59661.jpg?w=300&h=300)