Archives du mot-clef Pythagore

La BODYS : ajouts dans l’onglet « Démontrer / Justifier » (en Maths)

Publié le par
Répondre

2 ajouts dans cette partie importante de la démonstration en maths .

  1. Attention : Toutes les cartes et méthodes utilisées sont disponibles en entier dans les articles sur la droite des milieux (ici) et sur le théorème de Pythagore (ici et là et encore là) , alors que dans les images ci-dessous elles n ‘apparaissent pas en entier
  2. Ci-dessous ce sont des « images » (donc souvent incomplètes pour pouvoir les mettre avec la capture d’écran) de la BODYS ESSAI

1- La droite des milieux : 3 démonstrations

page 1 : la droite des milieux et à quoi ça sert : 2 cartes mentales

 

pages 2 à 4 : démonstrations avec la droite des milieux et ses propriétés dans un triangle quelconque (avec méthode identique en 3 points : Je sais que / Or / Donc)

page 2 : démontrer qu’un point est le milieu d’un segment

page 3 : calculer la longueur d’un segment

page 4 : démontrer que 2 droites sont parallèles

2- Le théorème de Pythagore : 2 démonstrations, 1 vérification

page 1 : Le théorème de Pythagore en carte mentale

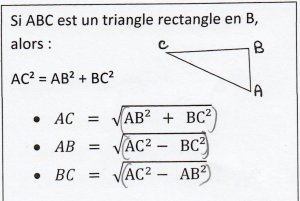
page 2 : Calculer la mesure d’un côté d’un triangle rectangle et fiche d’aide

page 3 : Vérifier les mesures des côtés d’un triangle rectangle

page 4 : Démontrer qu’un triangle est rectangle ou non (avec Pythagore et avec les angles)

Une BODYS toujours à l’essai ….. J’essaie de mettre au fur et à mesure des méthodes, fiches d’aide, des procédures qui nous sont utiles cette année en vue aussi de l’année prochaine . Même si Léo ne s’en sert pas en classe , on l’a au moins sous la main à la maison et lors des révisions …. Nous poursuivrons l’onglet « démontrer / justifier » au fur et à mesure des notions étudiées en classe .

Pythagore : une autre piste d’automatisation dans le calcul de la mesure d’un côté

Publié le par
Répondre

Après les articles précédents sur Pythagore (ici et là) , voici une autre aide donnée en classe qui peut permettre la « flexibilité », la mémorisation ….. :

Dans le triangle ABC rectangle en B  , on a :

  

DONC pour calculer la mesure des côtés de ce triangle , on peut directement appliquer les « formules » . Néanmoins, pour Léo , il m’a semblé encore nécessaire d’avoir tout par écrit, d’entourer (ou surligner) ce que l’on cherche et d’utiliser le « geste » qui cache (ou enlève) un des termes …. [quand ce n’est pas la mesure de l’hypoténuse qui est cherchée, cas le plus simple)]. Le « carré » aussi qui parfois disparaît …… Il faut être en mesure d’expliquer ce que l’on fait pour pouvoir mémoriser une démarche et l’automatiser ….

Une autre piste : peut-être, pourrait-on passer par une étape intermédiaire de type  :

Document à télécharger sous Word  Utiliser Pythagore METHODE 

à ajouter dans nos fiches d’aide aux démonstrations en lien avec Pythagore ( voir les 2 1ères ici ) et dans la BODYS ( à venir dans un prochain article) …… On devrait en avoir besoin encore en 3ème au moins ….

Plus de clarté en image dans un exercice « guidé » mais où je demande à Léo d' »expliciter » sa démarche, de bien visualiser et faire des liens avec le »dessin , codage » du triangle rectangle , pour automatiser MAIS en réfléchissant ….. oralement au moins même si c’est plus long ….. Le travail ici est de « vérifier » les mesures des 3 côtés grâce à l’égalité de Pythagore :

Exercice fait  en image :

exercice d’entraînement à télécharger sous Word Vérifier les mesures de chaque côté EXO

Parallèlement, nous allons reprendre un exercice de chacune des démonstrations en utilisant le théorème de Pythagore  :

  • calcul d’une mesure d’un côté d’un triangle en connaissant les 2 autres
  • reconnaître si un triangle est rectangle

Il ne reste plus qu’à s’y mettre …… difficile pendant les vacances de Noël …..

 

Pythagore : un essai de démonstration de base

Publié le par
Répondre

En travaillant à nouveau avec le théorème de Pythagore ( article précédent ici ), nous avons essayé de procéder de manière « simple et rigoureuse » .

Trouver la longueur d’un côté

J’ai préparé une « fiche guide » (procédure, aide …. comme on voudra) pour installer une démarche en 3 étapes (la dernière étant la phrase réponse) . En image :

à télécharger sous Word PYTHAGORE PROCEDURES2

Démontrer qu’un triangle est rectangle (ou non )

2ème fiche , en image

( le carré jaune est pour indiquer le signe , s’il y a égalité ou non)

ça coince encore ????

Là où ça coince (et ce n’est sûrement pas spécifique aux enfants DYS ! ) :

  1. Passer de BC² à BC  : revenir au carré avec la surface connue , quand on doit trouver la longueur du côté pour arriver à : BC =√BC² ( si je sais que BC² = 33 alors BC = √33  . On peut aussi reprendre que le carré de √33 c’est 33 ….. à entraîner ….. mais le mélange est vite là !!!! on peut reprendre les fiches ici)
  2. Quand la longueur cherchée se trouve du côté de la somme des 2 termes au carré : une difficulté à « gérer » ( à chacun de trouver « sa » méthode ex : trouver BC quand on sait que AB² = AC² + BC² et que l’on connaît AB et AC : addition à trou ou soustraction ?…..)

Il nous faudra encore un peu de temps pour « automatiser » tout cela ……. et/ou trouver sa « propre » voie

Premiers pas avec Pythagore

Publié le par
1

Pythagore ou Paul Pogba ? à vous de choisir ……

Nous abordons ce fameux théorème qui va sans doute nous poursuivre au moins jusqu’en 3ème donc il faut bien commencer par l’apprivoiser ….. Pour cela , 2 notions sont à bien « recentrer » : le triangle rectangle et d’autre part la relation entre un nombre et son carré (pour pouvoir ensuite trouver la longueur d’un côté en « prenant » la racine ….)

une vue d’ensemble …..

avec cette carte où l’on a essayé de revoir le « sujet » dans son ensemble pour ensuite venir « zoomer » les différents points :

  • explications : qui était Pythagore ? Ce qu’il a démontré ? Une image pour nous aider : le fameux « dab » de Paul Pogba ( trouvé sur internet, explication de ce choix par un professeur de Mathématiques à lire ici)
  • ce théorème s’applique toujours dans un triangle rectangle

zoom sur le triangle rectangle

  • comment le reconnaître « visuellement » ? : avec son angle droit
  • savoir repérer l’hypothénuse : c’est très important ! Je n’ai pas choisi d’ajouter une « image mentale » pour l’hypothénuse  car simplement l’observation a suffi (même si dans un premier temps elle se distingue en vert sur la carte) : Léo se sert de sa taille pour la repérer (c ‘est le plus grand côté) ou bien de sa place par rapport à l’angle droit . On a fait quelques exercices où on donnait la « lettre » de l’angle droit , ou bien l’expression de Pythagore et il fallait placer les lettres …. Bref, on a manipulé un peu …..
  • On a revu aussi la propriété des angles dans un triangle : leur somme vaut 180° ce qui a permis de voir si un triangle était rectangle ou non quand on connaît la mesure de 2 de ses angles ….
  • attention au vocabulaire à bien faire préciser : l’hypothénuse, un angle droit (et non pas rectangle ) , les côtés de l’angle droit
  • si nécessaire : reprendre la construction du triangle rectangle

Zoom sur le nombre , son carré et la racine carrée d’un autre

quelques points à reprendre et à « manipuler » dans sa tête pour obtenir la flexibilité nécessaire à son utilisation :

  • en partant du plus simple : 9² c’est 9X9 = 81 , DONC √81 c’est 9
  • en utilisant « la géométrie » : l’aire d’un carré (c X c ) est de 81cm² , son côté (c) c’est √81, donc c’est 9 cm
  • aide avec « image »
  • enfin toujours en géométrie , pour trouver la mesure d’un segment quand on connaît le carré de sa mesure : AB² = 81 donc AB = √81 = 9
  • Pour s’entraîner ( à plastifier) : on peut mettre soit des nombres , soit des lettres, soit des segments ….

zoom sur le théorème

  • savoir l’écrire en « phrase » : on attendra la « version exacte » qui sera donnée en classe
  • savoir l’écrire en « expression littérale » après avoir reconnu l’hypothénuse :

AB² = AC² + CB² (et inversement , pour arriver ensuite à manipuler à l’intérieur de l’égalité ….. on verra plus tard ….)

  • savoir à quoi sert ce théorème
  • un essai de fiche « procédure » pour soutenir la réflexion et l’ordre des « étapes » :

des outils à tester donc ……

à télécharger sous Word  Le théorème de Pythagore nombre et son carré entr Procédure pour appliquer un théorème ex Pythagore 2